Trended Lomb-Scargle Periodogram¶
The standard Lomb-Scargle methods in gatspy
(LombScargle, LombScargleFast,
and LombScargleAstroML)
fit a sinusoidal model to the data by minimizing the (weighted) squared
residuals. These methods also support a floating mean term,
which is an additional parameter that estimates the mean of the underlying
model. The TrendedLombScargle class extends
LombScargle by adding a trend parameter
that is linear in time. Such a parameter may be appropriate when the underlying
time series exhibits some non-stationarity.
API of Trended Lomb-Scargle Model¶
The TrendedLombScargle class has the same API as
LombScargle; the only difference is the underlying
model that is fit to the data.
Trended Lomb-Scargle Example¶
In order to motivate the trended Lomb-Scargle model, we’ll start with a one r-band RR Lyrae lightcurve and examine the effect of adding a linear trend on the estimated period. First, we’ll estimate the period as in Lomb-Scargle Periodogram before we add the trend:
In [1]: from gatspy import datasets, periodic
In [2]: rrlyrae = datasets.fetch_rrlyrae()
In [3]: lcid = rrlyrae.ids[0]
In [4]: t, mag, dmag, filts = rrlyrae.get_lightcurve(lcid)
In [5]: mask = (filts == 'r')
In [6]: t_r, mag_r, dmag_r = t[mask], mag[mask], dmag[mask]
In [7]: model = periodic.LombScargleFast(fit_period=True)
In [8]: model.optimizer.period_range = (0.2, 1.2)
In [9]: model.fit(t_r, mag_r, dmag_r);
In [10]: old_best_period = model.best_period
In [11]: old_best_period
Out[11]: 0.61431661211675215
The estimated period matches the period measured by Sesar 2010 to within
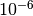 days.
days.
Now we will add a small linear trend to the observed data and see how the estimated period is affected:
In [12]: slope = 0.005
In [13]: mag_r += slope * (t_r - t_r[0])
In [14]: model.fit(t_r, mag_r, dmag_r);
In [15]: new_best_period = model.best_period
In [16]: model.score([old_best_period, new_best_period])
Out[16]: array([ 0.02881256, 0.87998659])
The addition of a small linear trend has greatly changed the estimated period;
in fact, the old best period now has very little power in the estimated
periodogram. Now let’s instead include a trend parameter by using the
TrendedLombScargle model:
In [17]: tmodel = periodic.TrendedLombScargle(fit_period=True)
In [18]: tmodel.optimizer.period_range = (0.2, 1.2)
In [19]: tmodel.fit(t_r, mag_r, dmag_r);
In [20]: trended_model_best_period = tmodel.best_period
In [21]: trended_model_best_period
Out[21]: 0.61431593030890863
The new trend parameter accounts for the linear increasing trend in the data, and we once again recover the original estimated period.