Odds Ratio for Cauchy vs Gaussian

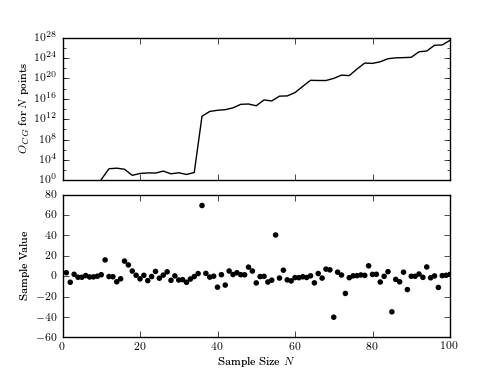
Figure 5.19

The Cauchy vs. Gaussian model odds ratio for a data set drawn from a Cauchy distribution (mu = 0, gamma = 2) as a function of the number of points used to perform the calculation. Note the sharp increase in the odds ratio when points falling far from the mean are added.

Code output:

Results for first 10 points:
  L(M = Cauchy) = 1.18e-12 +/- 1.92e-16
  L(M = Gauss)  = 8.09e-13 +/- 1.32e-16
  O_{CG} = 1.45 +/- 0.000237

Python source code:

# Author: Jake VanderPlas
# License: BSD
#   The figure produced by this code is published in the textbook
#   "Statistics, Data Mining, and Machine Learning in Astronomy" (2013)
#   For more information, see http://astroML.github.com
#   To report a bug or issue, use the following forum:
#    https://groups.google.com/forum/#!forum/astroml-general
import numpy as np
from matplotlib import pyplot as plt
from scipy.stats import cauchy, norm
from scipy import integrate

#----------------------------------------------------------------------
# This function adjusts matplotlib settings for a uniform feel in the textbook.
# Note that with usetex=True, fonts are rendered with LaTeX.  This may
# result in an error if LaTeX is not installed on your system.  In that case,
# you can set usetex to False.
from astroML.plotting import setup_text_plots
setup_text_plots(fontsize=8, usetex=True)


def logL_cauchy(xi, gamma, mu,
                mu_min=-10, mu_max=10, sigma_min=0.01, sigma_max=100):
    """Equation 5.74: cauchy likelihood"""
    xi = np.asarray(xi)
    n = xi.size
    shape = np.broadcast(gamma, mu).shape

    xi = xi.reshape(xi.shape + tuple([1 for s in shape]))

    prior_normalization = - (np.log(mu_max - mu_min)
                             + np.log(np.log(sigma_max / sigma_min)))

    return (prior_normalization
            - n * np.log(np.pi)
            + (n - 1) * np.log(gamma)
            - np.sum(np.log(gamma ** 2 + (xi - mu) ** 2), 0))


def logL_gaussian(xi, sigma, mu,
                  mu_min=-10, mu_max=10, sigma_min=0.01, sigma_max=100):
    """Equation 5.57: gaussian likelihood"""
    xi = np.asarray(xi)
    n = xi.size
    shape = np.broadcast(sigma, mu).shape

    xi = xi.reshape(xi.shape + tuple([1 for s in shape]))

    prior_normalization = - (np.log(mu_max - mu_min)
                             + np.log(np.log(sigma_max / sigma_min)))

    return (prior_normalization
            - 0.5 * n * np.log(2 * np.pi)
            - (n + 1) * np.log(sigma)
            - np.sum(0.5 * ((xi - mu) / sigma) ** 2, 0))


def calculate_odds_ratio(xi, epsrel=1E-8, epsabs=1E-15):
    """
    Compute the odds ratio by perfoming a double integral
    over the likelihood space.
    """
    gauss_Ifunc = lambda mu, sigma: np.exp(logL_gaussian(xi, mu, sigma))
    cauchy_Ifunc = lambda mu, gamma: np.exp(logL_cauchy(xi, mu, gamma))

    I_gauss, err_gauss = integrate.dblquad(gauss_Ifunc, -np.inf, np.inf,
                                           lambda x: 0, lambda x: np.inf,
                                           epsabs=epsabs, epsrel=epsrel)
    I_cauchy, err_cauchy = integrate.dblquad(cauchy_Ifunc, -np.inf, np.inf,
                                             lambda x: 0, lambda x: np.inf,
                                             epsabs=epsabs, epsrel=epsrel)

    if I_gauss == 0:
        O_CG = np.inf
        err_O_CG = np.inf
    else:
        O_CG = I_cauchy / I_gauss
        err_O_CG = O_CG * np.sqrt((err_gauss / I_gauss) ** 2)

    return (I_gauss, err_gauss), (I_cauchy, err_cauchy), (O_CG, err_O_CG)


#------------------------------------------------------------
# Draw points from a Cauchy distribution
np.random.seed(44)
mu = 0
gamma = 2
xi = cauchy(mu, gamma).rvs(100)

#------------------------------------------------------------
# compute the odds ratio for the first 10 points
((I_gauss, err_gauss),
 (I_cauchy, err_cauchy),
 (O_CG, err_O_CG)) = calculate_odds_ratio(xi[:10])

print "Results for first 10 points:"
print "  L(M = Cauchy) = %.2e +/- %.2e" % (I_cauchy, err_cauchy)
print "  L(M = Gauss)  = %.2e +/- %.2e" % (I_gauss, err_gauss)
print "  O_{CG} = %.3g +/- %.3g" % (O_CG, err_O_CG)

#------------------------------------------------------------
# calculate the results as a function of number of points
Nrange = np.arange(10, 101, 2)
Odds = np.zeros(Nrange.shape)
for i, N in enumerate(Nrange):
    res = calculate_odds_ratio(xi[:N])
    Odds[i] = res[2][0]

#------------------------------------------------------------
# plot the results
fig = plt.figure(figsize=(5, 3.75))
fig.subplots_adjust(hspace=0.1)

ax1 = fig.add_subplot(211, yscale='log')
ax1.plot(Nrange, Odds, '-k')
ax1.set_ylabel(r'$O_{CG}$ for $N$ points')
ax1.set_xlim(0, 100)
ax1.xaxis.set_major_formatter(plt.NullFormatter())
ax1.yaxis.set_major_locator(plt.LogLocator(base=10000.0))

ax2 = fig.add_subplot(212)
ax2.scatter(np.arange(1, len(xi) + 1), xi, lw=0, s=16, c='k')
ax2.set_xlim(0, 100)
ax2.set_xlabel('Sample Size $N$')
ax2.set_ylabel('Sample Value')

plt.show()

[download source: fig_odds_ratio_cauchy.py]